Java.com.mk

Рендерирање

Една од предностите на Java 2D API-то е тоа што облиците, текстот и сликите можат да бидат манипулирани, во поголем дел, на ист начин. Четирите делови од процесот на рендерирање (rendering pipeline) кои се извршуваат на секој графички објект се:
·    трансформирање (transforming) – секој графички објект може да биде трансформиран како што се рендерира. Трансформациите вклучуваат трансалции, ротации, скалирање, делење (shearing) или пак комбинација од сите четири.

·    соединување (compositing) – процес на соединување/компонирање на сите делови од некоја слика во една целина. Java 2D API-то дефинира доста корисни правила на композиција и овозможува деловите од сликата да бидат транспарентни во целост или пак само одредени делови.

·    clipping – понекогаш несакаме да цртаме надвор од некоја област, на пример сакаме да се исцрта дел од слика која е видлива од рамката на некоја врата. Оваа операција се нарекува clipping. Java 2D API-то да се дефинира било каков облик (Shape) како рамка.

·    rendering hints – antialiasing е техника која се користи за измазнување на грубите рабови од некоја слика. Рендерирачката машина овозможува antialiasing и други брзи и квалитетни техники кои го подобруваат квалитетот на сликата преку механизмот наречен rendering hints.

Ние, најмногу ќе се задржиме на трансформациите кои можат да се направат во процесот на рендерирање.

Трансформирање (Transforming)

Класата java.awt.geom.AffineTransform ги претставува трансформациите во 2D APIто. Под affine трансформација се подразбира дека после трансформацијата паралелните линии ќе останат паралелни. Graphic2D рендерирачката машина има своја внатрешна AffineTransform која ја додава на графичките објекти при нивното рендерирање. Можеме да ја поставиме или модифицираме оваа трансформација преку методите:
·    Public abstract void setTransform(AffineTransform Tx) – поставува моментална трансформација
·    Public abstract void transform(AffineTransform Tx) – ја модифицира моменталната трансформација со некоја нова Tx.

Важно: Подобро е да ја модифицираме тековната трансформација отколку да ја смениме со нова.

Нова AffineTransform може да креираме користејќи го конструкторот:
public AffineTransform()

Значи постојат два начина на кои можеме да трансформираме еден графички објект. Едниот е преку модифицирање во Graphics2D, со што оставаме на машината да се погрижи за деталите. Вториот начин е ние да го трансформираме секој објект посебно и потоа да го рендерираме. Што ќе избереме зависи од потребите.
Ако сакаме сами да ги правиме трансформациите (без менување во Graphics2D) следниве методи ќе ни бидат корисни:
·    public Point2D transform(Point2D ptSrc, Point2D ptDst) – го трансформира ptSrc и промените ги чува во ptDst.
·    public Shape createTransformedShape(Shape pSrc) – прави трансформации и го враќа резултатот.

Транслација

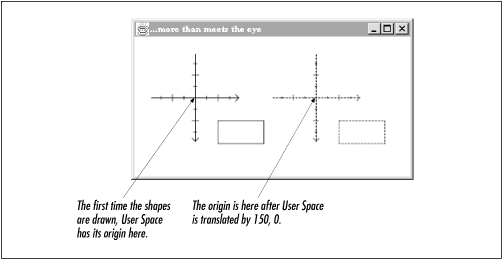
Една од основните типови на трансформации е транслацијата. Едноставно кажано, транслацијата е процес на преместување/движење на координатниот систем со што неговиот почеток е на ново место. Следната слика го покажува ефектот на транслација:

Има неколку методи во AffineTransform повржани со транслација. Притоа можеме да додадеме транслација на веќе постоечка трансформација или пак да креираме нова:
·    public void translate(double tx, double ty) – додава tx и ty транслација на AffineTransform.
·    public void setToTranslation(double tx, double ty) – ја поставува тековната AffineTransform да претставува транслација за tx и ty.
·    public static AffineTransform getTranslateInstance(double tx, double ty) – овој метод креира нова AffineTransform и ја иницијализира да претставува транслација користејќи го даденото поместување.

Ротација

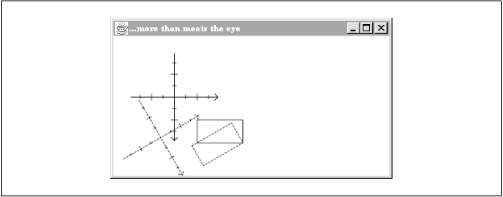
Уште една основна трансформација е ротацијата. Сликата подолу претставува ротација за Pi/6 радијани. Трансформираната форма претставена е со испрекинати линии.

Ротацијата може да се изврши околу секоја точка. Во примерот наведен погоре, ротацијата се врши околу координатниот почеток. Ротација околу било која друга точка е транслирана ротација. На наредната слика е прикажана ротација за Pi/6 околу долниот десен агол на правоаголникот:

Класата AffineTransform нуди корисни методи за работа со ротација и транслирана ротација:
·    public void rotate(double theta) – овој метод додава ротација на тековната AffineTransform. Дадениот агол е во радијани.
·    public void rotate(double theta, double x, double y) – овој метод додава транслирана ротација. Ротацијата ќе се изврши околу дадената точка.
·    public void setToRotation(double theta) – ја поставува AffineTransform трансформацијата да претставува ротација за theta радијани.
·    public void setToRotation(double theta, double x, double y) - ја поставува AffineTransform трансформацијата да претставува транслирана ротација.
·    public static AffineTransform getRotateInstance(double theta) – креира нов AffineTransform објект и го инизијализира да претставува ротација.
·    public static AffineTransform getRotateInstance(double theta, double x, double y) - креира нов AffineTransform објект и го инизијализира да претставува транслирана ротација.

Скалирање

Скалирање е операција која ги прави објектите поголеми или помали. Се разбира дека AffineTransform има и методи кои го олеснуваат скалирањето:
·    public void scale(double sx, double sy) – овој метод додава скалирање на тековната AffineTransform трансформација. Факторот на скалирање треба да го претставува односто на новата големина со старата. На пример scale(1,1) нема да промени ништо, додека пак scale(0.5,0.5) ќе ги редуцира двете оски за 50%.
·    public void setToScale(double sx, double sy) – овој метод ја поставува тековната AffineTransform трансформација да претставува ротација користејќи ги sx и sy. Било која претходна трансформациај содржана во AffineTransform ќе биде избришана.
·    public static AffineTransform getScaleInstance(double sx, double sy) – овој метод креира нова AffineTransform трансформација и ја иницијализира да претставува скалирање користејќи ги дадените вредности. Ова е исто да се креира нов AffineTransform објект и да се повика setToScale().

Shearing

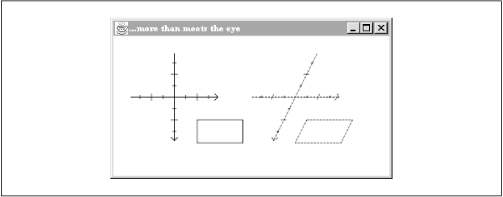
Последната фундаментална трансформација е shearing, каде што координатниот простор се развлекува паралелно со некоја од оските (или двете). Следнава слика најдобро ќе ја објасниоваа тренсформација:

Оваа трансформација е определена со два параметра, shx и shy, кои кажуваат колку да се развлечат x и y оската соодветно. Секоја точка (x, y) се трансформира во нова точка (x+(shx)y, y+(shy)x). На горната слика е претставен ефектот на shearing со параметри shx=-0.5 и shy=0.
Следниве методи од AffineTransform се користат при ваква трансформација:
·    public void shear(double shx, double shy)
·    public void setToShear(double shx, double shy)
·    public static AffineTransform getShearInstance(double shx, double shy)

Објаснувањето на овие методи е аналогно на методите од претходно наведените трансформации.

страна број: 1 2 3 4 5 6 7 8 9

<< претходна страна :

: следна страна >>